বুদ্ধিমত্তা বিস্ফোৰণ

বুদ্ধিমত্তা বিস্ফোৰণ (Intelligence Explosion)

জীৱনজ্যোতি বৰদলৈ, বেংগালুৰু

এসময়ত বোলে এখন দেশত এজন বৰ ন্যায়পৰায়ণ ৰজাই শাসন কৰিছিল। কোনো প্রজা যাতে ন্যায় বিচাৰৰ পৰা বঞ্চিত নহয়, তাৰ প্রতি তেওঁ সততে চকু ৰাখিছিল। পিছে হ’লে কি হ’ব, দেশৰ আইন ব্যৱস্থাত থকা অনেক সুৰুঙাৰ সুযোগ লৈ বহু চতুৰ অপৰাধী সাৰি গৈছিল আৰু বহু সময়ত নিৰ্দোষীজনেও শাস্তি পাবলগীয়া হৈছিল। এই কথাটো লৈয়েই ৰজাৰ বৰ আক্ষেপ। ঘটনাক্রমে এদিন ৰজাৰ হাতলৈ এখন যাদুকৰী পীৰা আহিল। এই পীৰাখনত উঠি কোনোবাই মিছা কথা কলে কওঁতাজনৰ চেহেৰা মুহূৰ্তৰ ভিতৰতে বিকৃত হৈ পৰিব। ৰজাৰ মনত অপাৰ আনন্দ! এতিয়াৰে পৰা আৰু কোনো অপৰাধী সাৰি যাব নোৱাৰিব, কোনো নিৰ্দোষীয়ে মিছাতে শাস্তি পাবলগীয়া নহ’ব। 

মহামন্ত্রীয়ে পিছে কথাটো বৰ ভাল নেপালে। তেওঁৰ মতে এনেধৰণৰ নিৰ্জীৱ-নিষ্প্রাণ বস্তু একোটাহঁতৰ ভৰষাত ইমান ডাঙৰ ডাঙৰ সিদ্ধান্ত লোৱা উচিত নহয়। দুনিয়াত এই পীৰাক ফাঁকি দিব পৰা মানুহো ওলাব। মন্ত্ৰীৰ কথা শুনি ৰজাৰ উঠিল উগ্ৰ খং। এইহেন মহান, ন্যায়ৰ প্ৰতীক পীৰাখনৰ এই অপমান? এমাহ সময় দিব তেওঁ। এই এমাহৰ ভিতৰত যদি মহামন্ত্ৰীয়ে তেওঁৰ কথা প্ৰমাণ কৰি দেখুৱাব নোৱাৰে, কথা বেয়া হ’ব। মহামন্ত্ৰীক চৰমসীমা বান্ধি দি ৰজা নিজৰ সিদ্ধান্তত অটল হৈ থাকিল আৰু ৰাজসভালৈ অহা প্রতিটো গোচৰৰ নিষ্পত্তি কৰিবলৈ পীৰাখন ব্যৱহাৰ কৰিবলৈ ললে। অচিৰেই ইয়াৰ সুফলো পোৱা গ’ল। 

এনেকৈয়ে এমাহ পাৰ হওঁ হওঁ হ’ল। এনেতে এদিন এটা বৰ আচৰিত ঘটনা ঘটিল। সেইদিনা ৰাজসভালৈ গোচৰ লৈ আহিল এগৰাকী মহিলা। সেই দেশৰ নতুন নিয়ম মতেই গুচৰীয়া মহিলাগৰাকীয়ে যাদুকৰী পীৰাখনত উঠি গোচৰ দিলে – বোলে এজন ভণ্ড সাধুৱে এৰাতিৰ ভিতৰতে দুগুণ কৰি দিম বুলি মহিলাৰ গোটেইসোপা গহনা-গাঁথৰি ৰাখি থলে। পিছদিনাখন কিন্তু সাধুৱে ওলোটা খৰ মাৰিবলৈ আৰম্ভ কৰিলে, তেখেতে বোলে মহিলাক সকলোবোৰ গহনা ঘূৰাই দিলেই! কিন্তু আচলতে সাধুৱে ফুটাকড়ি এটাও ঘূৰোৱা নাই! ইমানখিনি কথা কোৱাৰ পিছতো মহিলাৰ চেহেৰাৰ অলপো হেৰফেৰ নোহোৱা দেখি ৰাজসভাত থকা কাৰোৱেই বুজিবলৈ বাকী নেথাকিল যে সাধুজনে মহিলাক ঠগাৰ কথাটো সত্য। সাধুক ৰাজসভালৈ অনা হ’ল। বিচাৰৰ নিয়ম মতে যিহেতু অভিযুক্তজনকো আত্মপক্ষ সমৰ্থন কৰিবলৈ সুবিধা দিব লাগে, গতিকে সাধুকো পীৰাখনত উঠি উত্তৰ দিবলৈ কোৱা হ’ল। পীৰাখনত উঠিবলৈ যোৱাৰ আগে আগে সাধুজনে নিজৰ হাতত থকা লাঠিডাল ওচৰতে থকা গুচৰীয়া মহিলাগৰাকীকে ধৰিবলৈ দি থৈ গ’ল। পীৰাত উঠি সাধুৱে কলে বোলে তেওঁ অকণো মিছা কথা কোৱা নাই, মহিলাক ইতিমধ্যে গহনাবোৰ ঘূৰাই দিয়া হৈছে। সাধুৰ চেহেৰা যে সেই মুহূৰ্ততে বিকৃত হৈ পৰিব সেই কথাত কাৰো সন্দেহ নাছিল। কিন্তু আচৰিত কথা – মহিলাগৰাকীৰ দৰেই সাধুজনৰ চেহেৰাৰো অকণো পৰিৱৰ্তন নহ’ল! 

প্রধান বিচাৰক আছিল ৰজা নিজেই। তেওঁ মহা বিমোৰত পৰিল। এয়ানো কেনেকৈ সম্ভৱ? সেই সময়তে মহামন্ত্রীয়ে আহি সাধুৰ হাতৰ পৰা (ইতিমধ্যে সাধুৱে মহিলাৰ হাতৰপৰা লাঠিডাল আকৌ নিজৰ হাতত লৈ লৈছিল) লাঠিডাল লৈ সোঁমাজতে ভাঙি পেলালে। ফোপোলা লাঠিডালৰ ভিতৰৰ পৰা মহিলাৰ গহনা-গাঁথৰিবোৰ ওলাই পৰিল। 

এই সাধুটোত উল্লেখ কৰা পীৰাখনৰ দৰেই কম্পিউটাৰৰ দৰে যন্ত্র একোটাহঁতে পোনপটীয়া নিৰ্দেশ গ্রহণ কৰি, স্পষ্টকৈ যোগান ধৰা তথ্যৰ (যাক আমি ইনপুট বুলি কওঁ) ভিত্তিত মানুহতকৈ অনেকগুণ দক্ষতাৰে নিজৰ কাম সমাপণ কৰিব পাৰে। প্ৰকৃততে মানুহে হাতেৰে কৰা কামতকৈ অনেকগুণ দক্ষতাৰে কৰিব পৰা কাৰণেই আমি যন্ত্রৰ ব্যৱহাৰ কৰোঁ। কিন্তু নিৰ্দেশ আওপকীয়া হ’লেই, যোগান ধৰা তথ্য অলপ অস্পষ্ট হ’লেই যন্ত্রৰ লেঠা লাগে। সেই কাৰণেই যাদুকৰী পীৰাখনে মানুহৰ ছলনা বুজি নেপায় বা কম্পিউটাৰ প্র’গ্রাম একোটাই অকোঁৱা পকোৱাকৈ লিখা আখৰ পঢ়িবলৈ অসুবিধা পায়। 

কিন্তু সেয়া কৃত্ৰিম বুদ্ধিমত্তাৰ আগৰ কথা। কৃত্ৰিম বুদ্ধিমত্তা, বিশেষকৈ সৃজনীশীল কৃত্ৰিম বুদ্ধিমত্তা (Generative AI – যেনে আজিকালি অতি জনপ্ৰিয় হোৱা OpenAI ৰ ChatGPT বা Google ৰ Bard) অহাৰ লগে লগে যেন সকলো সলনি হ’বলৈ লৈছে। এইবিলাক ছফটৱেৰে কবিতা লিখাৰপৰা আৰম্ভ কৰি কম্পিউটাৰ প্ৰ’গ্ৰাম লিখি উলিউৱালৈকে সকলো কাম কৰিব পাৰে। কিন্তু কৃত্ৰিম বুদ্ধিমত্তানো কি?

যদি আমি মানুহৰ বা অন্যান্য কোনো জন্তুৰ বুদ্ধিমত্তাক স্বাভাৱিক বা প্ৰাকৃতিক বুদ্ধিমত্তা বুলি কওঁ, যন্ত্ৰ বা কম্পিউটাৰ পদ্ধতি একোটাহঁতৰ বুদ্ধিমত্তাক আমি কৃত্ৰিম বুদ্ধিমত্তা (Artificial Intelligence) বুলি ক’ব পাৰোঁ। কাৰণ সেই বুদ্ধিমত্তা মানুহে সৃষ্টি কৰা; বিৱৰ্তনৰ ফলত প্ৰাকৃতিকভাৱে আহৰণ কৰা বুদ্ধিমত্তা নহয়। কৃত্ৰিম বুদ্ধিমত্তা মানুহৰ বুদ্ধিমত্তাৰ সমপৰ্যায়ৰ এতিয়াও হোৱাগৈ নাই, কিন্তু যোৱা দশকটোৰ ভিতৰতে বিভিন্ন ক্ষেত্ৰত ইয়াৰ প্ৰয়োগ অতি দ্ৰুতগতিত বৃদ্ধি হ’বলৈ লৈছে। ইয়াৰ মূলতে আছে যন্ত্ৰ-শিক্ষণ (Machine Learning) নামৰ এক পদ্ধতিৰ দ্ৰুত বিকাশ। পৰিসংখ্যাবিজ্ঞানৰ বিভিন্ন সূত্ৰ-সঁজুলিৰ সহায়ত আমি ডাটাৰ পৰা ব্যৱহাৰযোগ্য অৰ্থ বিচাৰি উলিয়াব পাৰোঁ। আগতে এই ধৰণৰ ডাটা বিশ্লেষণৰ কামবোৰ খৰতকীয়াকৈ কৰিবলৈ কম্পিউটাৰ ব্যৱহাৰ কৰা হৈছিল ঠিকেই, কিন্তু সেই কম্পিউটাৰ প্ৰ’গ্ৰামবোৰৰ বুদ্ধিমত্তা আছিল তেনেই সীমিত। নতুন ধৰণৰ ডাটা আহি পৰিলেই প্ৰ’গ্ৰামবোৰ সলনি বা উন্নীত কৰিবলগীয়া হৈছিল। এক কথাত প্ৰ’গ্ৰামবোৰে মানুহৰ দৰে নতুন ডাটাৰপৰা ‘নিজে নিজে’ শিকি নিজৰ বুদ্ধিমত্তাৰ বিকাশ ঘটাই যাব নোৱাৰিছিল। কিন্তু আজি কালি সেয়া সলনি হৈছে। যন্ত্ৰ এটাক কৃত্ৰিম বুদ্ধিমত্তা প্ৰদান কৰাৰ অনেক উপায় আছে, কিন্তু বৰ্তমান সময়ত সবাতোকৈ জনপ্ৰিয় উপায়টো হৈছে এনে কিছুমান কম্পিউটাৰ প্ৰ’গ্ৰাম বা ছফটৱেৰ তৈয়াৰ কৰা যিবোৰে মানুহৰ দৰে নিজে নিজে ডাটাৰ পৰা শিকি নিজৰ বুদ্ধিমত্তাৰ বিকাশ ঘটাই যাব পাৰে। সেয়াই যন্ত্ৰ-শিক্ষণ।

কিন্তু যন্ত্ৰ বা কম্পিউটাৰ পদ্ধতি এটাই শিকে কেনেকৈ? এই কথা বুজিবলৈ আমি অলপ বীজগণিত আৰু পৰিসংখ্যাবিজ্ঞান জানি ল’ব লাগিব। ধৰা হওক x আৰু y দুটা চলক আৰু দুয়োটাই বাস্তৱ মান গ্ৰহণ কৰিব পাৰে। চলক x ৰ মান স্বতন্ত্ৰ কিন্তু চলক y ৰ মান নিৰ্ভৰ কৰে x ৰ মানৰ ওপৰত। তেনেহ’লে আমি y ক x ৰ ফলন (function) হিচাপে প্ৰকাশ কৰিব পাৰোঁ আৰু গাণিতিক ভাষাত এনেকৈ লিখিব পাৰোঁ: y = f(x), য’ত f হৈছে চলক x ৰ ফলন। যদি আমি এই ফলনটোৰ বীজগাণিতিক ৰূপ কি জানোঁ তেনেহ’লে x ৰ মান দিয়া থাকিলে y ৰ মান গণনা কৰি উলিয়াব পাৰোঁ। উদাহৰণস্বৰূপে যদি আমি জানোঁ যে y = f(x) = x2 তেনেহ’লে x ৰ মান ১ হ’লে y ৰ মান হ’ব ১, x ৰ মান 0.১ হ’লে y ৰ মান হ’ব 0.0১, x ৰ মান ২.৩ হ’লে y ৰ মান হ’ব ৫.২৯ ইত্যদি।

X	Y
-১	২.৫ x ১০-১৬ (প্ৰায় ০)
-০.৭৫	১
-০.৫	-১.২ x ১০-১৬ (প্ৰায় ০)
-০.২৫	-১
০	০
০.২৫	১
০.৫	১.২ x ১০-১৬ (প্ৰায় ০)
০.৭৫	-১
০.৮৭৫	?
১	-২.৫ x ১০-১৬ (প্ৰায় ০)
তালিকা - ১

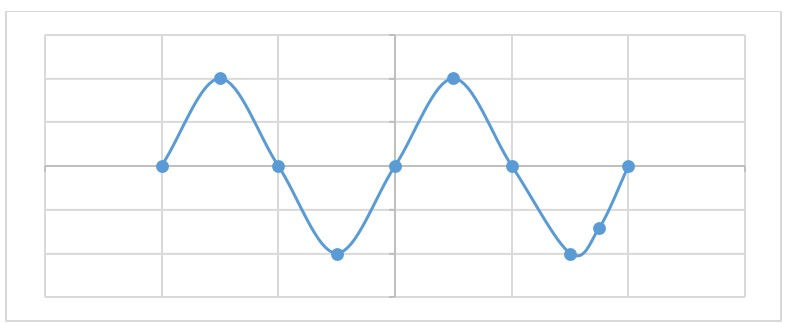
এইবাৰ এই তালিকাখনলৈ মন কৰিলে (তালিকা-১) দেখা যাব যে ইয়াত x ৰ কেইটামান মানৰ কাৰণে y ৰ মান কি হ’ব সেইটো দিয়া আছে। কিন্তু এইবাৰ আমাৰ ওচৰত কেৱল ডাটাখিনিহে আছে, প্ৰকৃত ফলনটো (অৰ্থাৎ x আৰু y ৰ মাজৰ সম্বন্ধটো) কি আমি নাজানোঁ। তালিকাখনত x ৰ এনে এটা মানো দিয়া হৈছে যাৰ কাৰণে y ৰ মান কি হ’ব সেইটো দিয়া হোৱা নাই (০.৮৭৫)। ফলনটো কি তাক নজনাকৈ y ৰ এই মানটো জনা সম্ভৱ হ’বনে? পৰিসংখ্যাবিজ্ঞানৰ মতে হ’ব পাৰে – ডাটাৰ গুণ আৰু পৰিমাণৰ ওপৰত নিৰ্ভৰ কৰি যথেষ্ট শুদ্ধকৈ এই মানটো কি সেইটো অনুমান কৰিব পৰা যাব পাৰে। কেনেকৈ পাৰি সেইটো চাবলৈ লগত দিয়া চিত্ৰখনলৈ মন কৰা যাওক (চিত্ৰ-১)। এই চিত্ৰখন আচলতে এখন লেখচিত্ৰ বা গ্ৰাফ(graph)। ইয়াত x-অক্ষত x ৰ মান আৰু y-অক্ষত y ৰ মান ৰাখি (x,y) ক্ৰমিক যোৰটোৱে বুজোৱা বিন্দু বিলাক দেখুউৱা হৈছে। ইয়াৰ পিছত এই বিন্দুকেইটাক সামৰি লোৱাকৈ এডাল বক্ৰ আঁকিবৰ যত্ন কৰা হৈছে। যদি আমাৰ হাতত থকা ডাটাবোৰ সম্পূৰ্ণ শুদ্ধ হয়, তেনেহ’লে প্ৰতিটো বিন্দুৱেই বক্ৰডালত থাকিব। পিছে বাস্তৱ উদাহৰণ কিছুমানৰ পৰা লোৱা ডাটাত অলপ ভেঁজাল থাকেই, গতিকে বাস্তৱক্ষেত্ৰত বহুকেইটা বিন্দু একেবাৰে বক্ৰডালৰ ওপৰতে নাথাকি অলপ ওচৰে-পাজঁৰে থাকিব। যি কি নহওক, আমি ধৰি ল’ব পাৰোঁ যে এই বক্ৰডালেই x আৰু yৰ ফলনটো বুজায়। এতিয়া xৰ যি কেইটা মানৰ কাৰণে yৰ মান তালিকাখনত দিয়া হোৱা নাই, সেইকেইটা মানৰ বাবে xৰ মানৰ পৰা বক্ৰডালত yৰ মান কি হ’ব গণনা কৰি উলিয়াব পাৰি। এই পদ্ধতিটোক সমাশ্ৰয়ণ (regression) বুলি জনা যায়।

চিত্ৰ - ১

আমাৰ উদাহৰণটোত y ৰ মান কেৱল এটা ৰাশিৰ ওপৰত নিৰ্ভৰশীল, সেইটো হ’ল x। কিন্তু বাস্তৱক্ষেত্ৰত আমি গণনা কৰি উলিয়াবলগীয়া ৰাশিটো অইন কেইবাটাও স্বতন্ত্ৰ ৰাশি বা কাৰকৰ (feature) ওপৰত নিৰ্ভৰ কৰিব পাৰে। উদাহৰণস্বৰূপে কোনো এজন ব্যক্তিৰ কোনো এবিধ বিশেষ ৰোগ হোৱাৰ সম্ভাৱনা নিৰ্ভৰ কৰে তেখেতৰ জেনেটিক গাঁথনিৰ পৰা আৰম্ভ কৰি খাদ্যাভ্যাস, বাস কৰা অঞ্চলটোৰ পৰিৱেশ ইত্যাদি অনেক কথাৰ ওপৰত। ডাটাৰ পৰা শিকিব পৰা কম্পিউটাৰ প্ৰ’গ্ৰাম এটাক প্ৰথমতে কিছুমান বাছি লোৱা ডাটাৰ সহায়ত প্ৰশিক্ষণ দিয়া হয়। এনে প্ৰশিক্ষণৰ বাবে ব্যৱহৃত ডাটাবোৰত কাৰক বা স্বতন্ত্ৰ ৰাশিবোৰৰ লগতে উলিয়াবলগীয়া ৰাশিটোৰ মানো দিয়া থাকে, যাক কোৱা হয় লেবেল (label) বুলি। ইয়াৰ পিছত যেতিয়া আচল কামৰ কাৰণে সেই প্ৰ’গ্ৰামটো ব্যৱহাৰ কৰা হয়, তেতিয়া সেই ডাটাবোৰত লেবেল অৰ্থাৎ উলিয়াবলগীয়া ৰাশিটো নাথাকে, সেইটো বিচাৰি বা গণনা কৰি উলিওৱাটো প্ৰ’গ্ৰামটোৰ কাম। যন্ত্ৰ-শিক্ষণৰ বাবে বহুতো দক্ষ এলগৰিথম (গণনা কৰা পদ্ধতি) উলাইছে। নিজৰ প্ৰশিক্ষণৰ দ্বাৰা লাভ কৰা জ্ঞান আৰু এনে এলগৰিথম প্ৰয়োগ প্ৰ’গ্ৰামটোৱে এই কামটো সমাধা কৰে। কেতিয়াবা সমাশ্ৰয়ণৰ সহায়ত এটা নিৰ্দিষ্ট ৰাশি গণনা কৰাৰ সলনি ডাটাবোৰক কিছুমান শ্ৰেণীৰ অন্তৰ্ভুক্ত কৰিব লগা হয়। এই পদ্ধতিক শ্ৰেণীবিভাজন (classification) বুলি কোৱা হয়।

শেহতীয়াকৈ কম্পিউটাৰ প্ৰ’গ্ৰাম একোটাহঁতে নিজেই কম্পিউটাৰ প্ৰ’গ্ৰাম লিখিবপৰা হৈছেগৈ। কিন্তু কম্পিউটাৰ এটাই কম্পিউটাৰ প্ৰ’গ্ৰাম এটা লিখাৰ অৰ্থ কি হ’ব পাৰে বাৰু? কম্পিউটাৰৰ বিৱৰ্তন? 

তাৰ মানে, মানুহে এসময়ত মানুহতকৈও বুধিয়ক যন্ত্ৰ সাজি উলিয়াব পাৰিবগৈ নেকি?

মানুহে যদি মানুহতকৈ অধিক বুধিয়ক যন্ত্ৰ সাজিব পাৰে, সেই বুধিয়ক যন্ত্ৰবোৰেও নিজতকৈ বেছি বুধিয়ক যন্ত্ৰ সাজি উলিয়াব পাৰিব – মানুহতকৈ কম সময়তে। সেই নতুন যন্ত্ৰবোৰে অকৌ তাতোকৈও অধিক দক্ষতাৰে নিজতকৈ অধিক বুধিয়ক আৰু দক্ষ যন্ত্ৰ সাজি উলিয়াব পাৰিব, নিচেই কম সময়ৰ ভিতৰতে। বিজ্ঞানীসকলে এই পৰিঘটনাটোক “বুদ্ধিমত্তা বিস্ফোৰণ” বা Intelligence Explosion বুলি অভিহিত

কৰিছে।

 @@@@@@@@@@@@